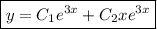а) Это однородное дифференциальное уравнение с постоянными коэффициентами. Перейдем к характеристическому уравнению, сделав замену
Решая как квадратное уравнение, получим
Общее решение:
б) Дифференциальное уравнение второго порядка с постоянными коэффициентами, однородное.
Пусть , получим характеристическое уравнение:
в) Пусть получим следующее характеристическое уравнение:
- корень характеристического уравнения кратности 2
а) Это однородное дифференциальное уравнение с постоянными коэффициентами. Перейдем к характеристическому уравнению, сделав замену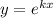
Решая как квадратное уравнение, получим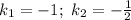
Общее решение: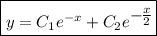
б) Дифференциальное уравнение второго порядка с постоянными коэффициентами, однородное.
Пусть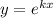 , получим характеристическое уравнение:
, получим характеристическое уравнение:
Общее решение: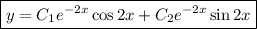
в) Пусть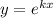 получим следующее характеристическое уравнение:
получим следующее характеристическое уравнение:
Общее решение: