Правильное условие : длина дороги 10 2/7(дробь)км. Заасфальтированная часть дороги составляет 5/7(дробь) не заасфальтированной части. Сколько километров составляет каждая часть?
Обозначим не заасфальтированную часть как х км, тогда
P(орел не выпал ни разу) = Р(орел выпал 0 раз) = .
2). Орел выпал неизвестно сколько раз, но точно не 2 раза.
Такому событию благоприятствуют события: "орел выпал 0 раз", "1 раз", "3 раза", "4 раза". Тогда вероятность равна сумме вероятностей всех этих элементарных событий, или же единице минус "орел выпал 2 раза" (так как сумма всех элементарных событий случайного эксперимента равна 1):
3). Решка выпала менее четырех раз.
Событие "решка выпала менее четырех раз" = событие "орел выпал больше нуля раз". И вероятность такого события равна единице минус вероятность события "орел выпал ноль раз":
6 км и 4 2/7 км
Пошаговое объяснение:
Правильное условие : длина дороги 10 2/7(дробь)км. Заасфальтированная часть дороги составляет 5/7(дробь) не заасфальтированной части. Сколько километров составляет каждая часть?
Обозначим не заасфальтированную часть как х км, тогда
заасфальтированная будет 5/7х км
Вся дорога 10 2/7=72/7 км
Получим уравнение:
х+5/7х=72/7
1 5/7 х= 72/7
12/7х=72/7
х=72/7 : 12/7
х=72/7 * 7/12
х=6 км не заасфальтированная часть дороги
заасфальтированная часть составит
5/7 * 6=30/7=4 2/7 км
ответ 6 км и 4 2/7 км
ответ: 1).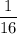 . 2).
. 2).  . 3).
. 3). 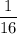 .
.
1). Орел не выпал ни разу.
P(орел не выпал ни разу) = Р(орел выпал 0 раз) =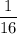 .
.
2). Орел выпал неизвестно сколько раз, но точно не 2 раза.
Такому событию благоприятствуют события: "орел выпал 0 раз", "1 раз", "3 раза", "4 раза". Тогда вероятность равна сумме вероятностей всех этих элементарных событий, или же единице минус "орел выпал 2 раза" (так как сумма всех элементарных событий случайного эксперимента равна 1):
3). Решка выпала менее четырех раз.
Событие "решка выпала менее четырех раз" = событие "орел выпал больше нуля раз". И вероятность такого события равна единице минус вероятность события "орел выпал ноль раз":